Recognition
Hao Su
Fall, 2021
Agenda
Semantic Understanding
Recognition: Draw Understanding From Images

We take image classification as the example understanding task.
Example Image Classification Challenge (CIFAR10)
- Task: Given an image, label it as one of the predefined semantic categories
- In CIFAR10, each image is given as a $32\times 32\times 3$ matrix.

Recognition is Difficult
- Semantic gap: The gap between low-level machine readable data and high-level human readable representation
- Can we hard-code rules to do recognition by
if-else
? Usually very hard. - Let us try to describe the appearance of
cats
Challenge: Change of Viewpoint
Challenge: Illumination

Challenge: Deformation

Challenge: Occlusion

Challenge: Background Clutter

Challenge: Intraclass Variation

From Model-Driven to Data-Driven
Model-Driven v.s. Data-Driven
In previous lectures, we were able to build models by deduction to solve a problem. For example:
- we use our knowledge of geometry to derive the camera model, which is a projective transformation
- we use our knowledge of analysis to derive the optical flow equation, which is a linear constraint
Model-Driven v.s. Data-Driven
To build models for these problems, our physics knowledge of how light is transported and how an image is formed is basically sufficient:
Forward problem (image formation):
- light transport
- perspective transformation
Inverse problem (3D and motion estimation):
- 3D reconstruction
- optical flow estimation
We build models based on
knowledge of physics!
knowledge of physics!
Model-Driven v.s. Data-Driven
However, for recognition problems, we do not have the exact forward model (e.g., from physics) that allows us to describe how raw image pixels are related with semantic categories.
Instead, we take a
data-driven approach.
data-driven approach.
Basic Paradigm of Data-Driven Method
The philosophy of data-driven people:
Why can we humans recognize cats? Because we have experience seeing cats in other scenarios.
Today, the study of data-driven method in CS is called
Machine Learning.
Train-Test Split
You might have heard that
I trained a machine learning model. What is training?
In machine learning for image classification, we have two sets of data: training data and testing data.

Example: In CIFAR10,
- training set: 50,000 images in total (5,000 images per category)
- test set: 10,000 images in total (1,000 images per category)

Machine Learning: Data-Driven Approach
- Collect a dataset of images and labels
- Use Machine Learning algorithms to train a classifier
- Evaluate the classifier on new images
def train(images, labels):
# machine learning!
return model
def predict(model, test_images):
# use model to predict labels
return test_labels

Stanford CS231n, Lecture 2
First classifier: Nearest Neighbor Method
def train(images, labels):
# machine learning!
return model
$\longrightarrow$ Memorize all data and labels
def predict(model, test_images):
# use model to predict labels
return test_labels
$\longrightarrow$ Predict the label of the most similar training image
First classifier: Nearest Neighbor Method
 Distance metric:
Distance metric:

Distance Metric to Compare Images
\[
d_1(I_1, I_2)=\sum_i |I_1^i-I_2^i| \tag{$L_1$ distance}
\]


Distance Metrics
Many possible choices of distance metrics:
\[
d_1(I_1, I_2)=\sum_i |I_1^i-I_2^i| \tag{$L_1$ distance}
\]
\[
d_2(I_1, I_2)=\sqrt{\sum_i |I_1^i-I_2^i|^2} \tag{$L_2$ distance}
\]
\[
d_{\infty}(I_1, I_2)=\max_i |I_1^i-I_2^i| \tag{$L_{\infty}$ distance}
\]
In general, we can define the $L_p$ distance:
\[
d_2(I_1, I_2)=\sqrt[p]{\sum_i |I_1^i-I_2^i|^p} \tag{$L_p$ distance}
\]

Nearest Neighbor classifier

Nearest Neighbor classifier
Memorize training data
Memorize training data
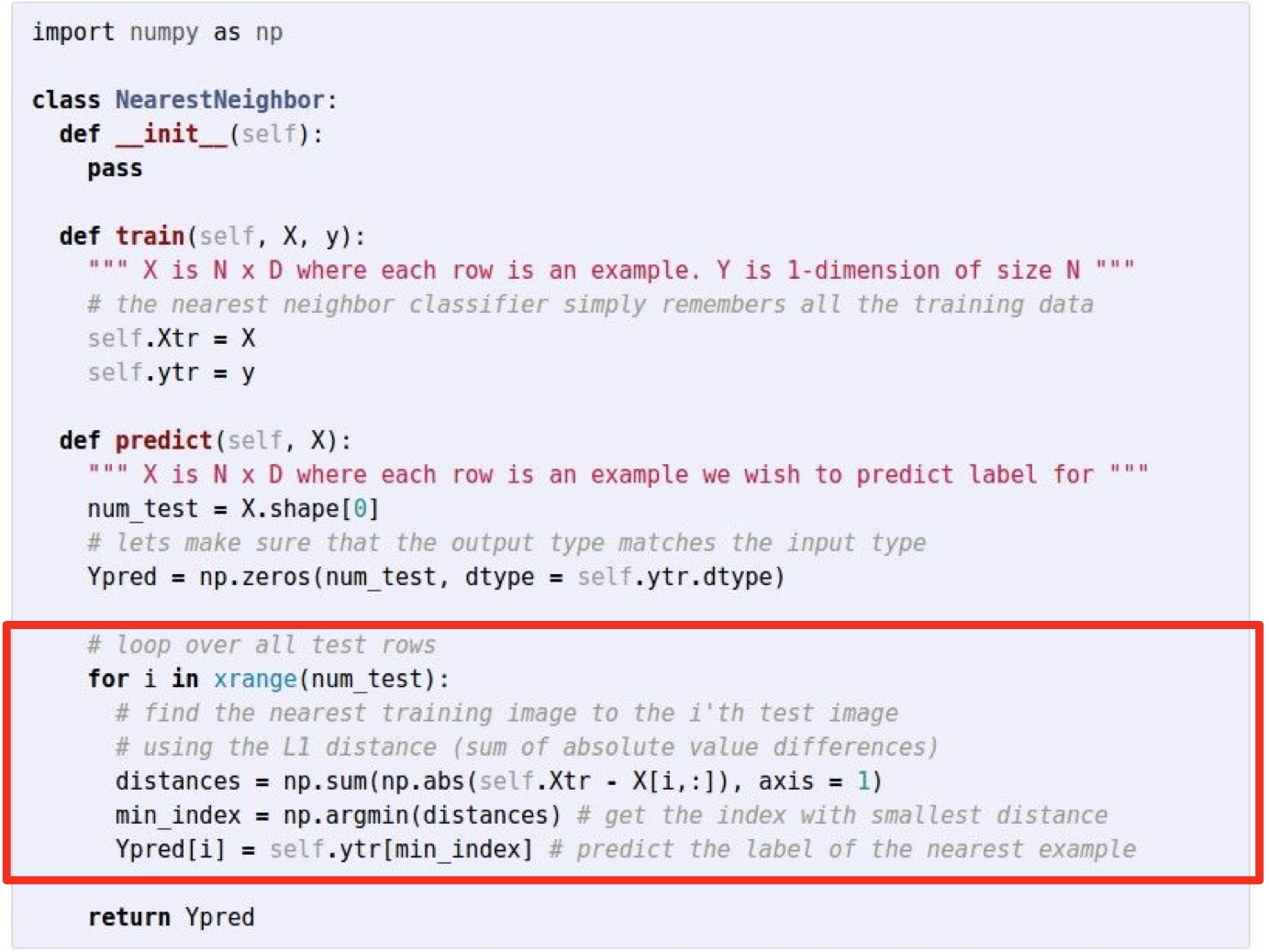
Nearest Neighbor classifier
For each test image:
Find closest train image
Predict label of nearest image
For each test image:
Find closest train image
Predict label of nearest image

Nearest Neighbor classifier
Q: With $N$ examples, how fast are training and prediction?
Q: With $N$ examples, how fast are training and prediction?
A: Train $\mathcal{O}(1)$, predict $\mathcal{O}(N)$.
This is bad: we want classifiers that are fast at prediction; slow for training is ok
Example Results on CIFAR10

Example Results on CIFAR10

Mathematical Formulation of Classification
Data Samples and Labels
- A data sample is a vector $x\in\R{n}$
- e.g., we can represent an image as a $32\times 32\times 3=3072$ dimensional vector
- The data sample $x$ belongs to one of $C$ predefined categories
- e.g., $C=3$ for boat/cat/plane
- We use an integer $y\in \{1,\ldots, C\}$ to represent the groundtruth label of $x$. Each number corresponds to a category.
- e.g., $y=1$ for boat, $y=2$ for cat, $y=3$ for plane
Classifier
A classifier $f$ is a function that predicts the label for a data sample:
\[
y=f_{\theta}(x)
\]
where $\theta$ is the parameter of $f$. For example, our nearest neighbor classifier has a parameter $p$ to denote the choice of $L_p$-distance.
Train and Test Set
- Train set: a set of $n_{train}$ data samples with labels \[ \mathcal{D}_{train}=\{(x_i, y_i)\}_{i=1}^{n_{train}} \]
- When we estimate the parameters $\theta$ of $f$, we can only use the train set
- Test set: a set of $n_{test}$ data samples with labels \[ \mathcal{D}_{test}=\{(x_i, y_i)\}_{i=1}^{n_{test}} \]
- When we evaluate the performance of a classifier, we can only use the test set
Prediction Accuracy, Train, Test
- On a dataset $\mathcal{D}$, the prediction accuracy is: \[ Acc_{\mathcal{D}}=\frac{\text{number of samples with the same groundtruth and predicted labels}}{\text{total number of samples in }\mathcal{D}} \]
- For the training procedure, we estimate $\theta$ on $\mathcal{D}_{train}$ so that $Acc_{\mathcal{D}_{train}}$ is maximized
- For the testing procedure, we run the classifier $f_{\theta}$ on $\mathcal{D}_{test}$ to compute $Acc_{\mathcal{D}_{test}}$
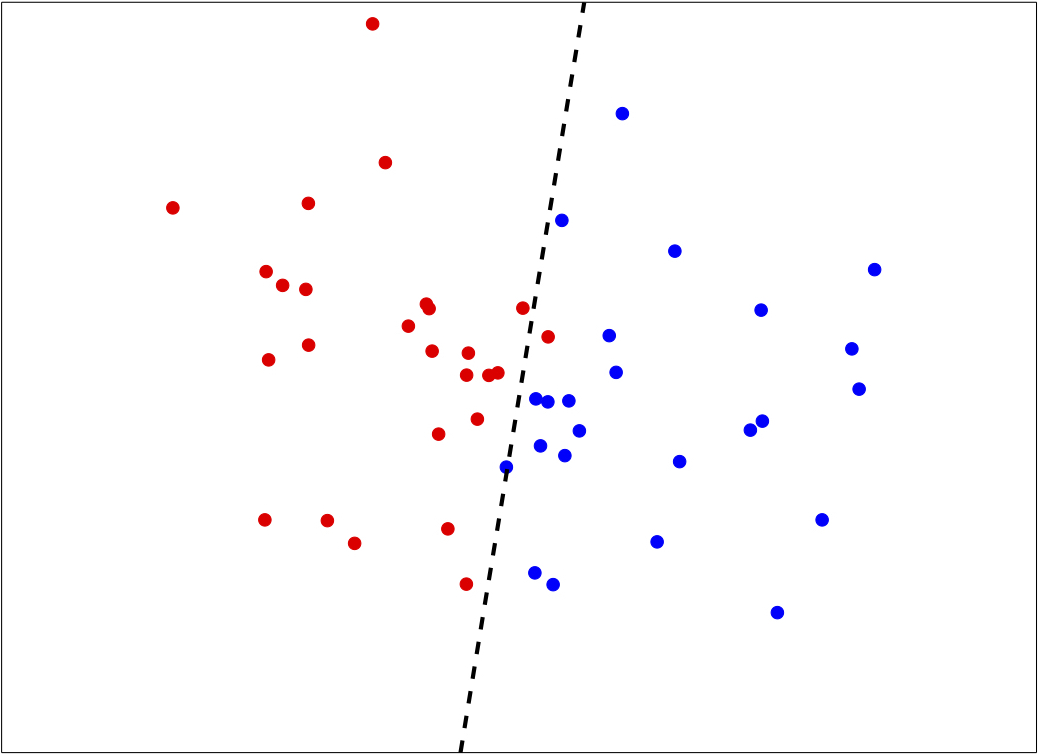
Geometric Visualization of a Classifier
- Consider a simplified classification problem: predict the label of 2D points on the plane.
- We plot the training data as points below. For each training data point $x$, the color indicates its class label.
- For any test point on the 2D plane, the predicted label by a nearest neighbor classifier is indicated by the color shading.

Linear Classifier
Linear Score Function
\[
f_{W,b}(x)=\underbrace{W}_{10\times 3072}\quad \underbrace{x}_{3072\times 1}+\underbrace{b}_{10\times 1}
\]
Example with an image with 4 pixels and 3 classes (cat/dog/ship):

Example with an image with 4 pixels and 3 classes (cat/dog/ship):

If $(W,b)$ is from a good classifier, it should give the highest score to the groundtruth class.
Geometric View of a Linear Classifier
Training Linear Classifier
Goal
For the linear classifier
\(
f_{W,b}(x)=Wx+b
\), find $(W,b)$ so that $f_{W,b}(x)$ performs well on the training data set
Plan
- First design a loss function of $(W,b)$ which represents the badness of prediction
- Then design an efficient algorithm to minimize the loss function (optimization)
Log-Likelihood Loss
Suppose: 3 training examples, 3 classes.
With some $(W,b)$ the scores $f_{W,b}(x)=Wx+b$ are:
With some $(W,b)$ the scores $f_{W,b}(x)=Wx+b$ are:

A loss function tells how good our current classifier is
Given a training set of examples
\[
\{(x_i, y_i)\}_{i=1}^{n_{train}}
\]
where $x_i$ is the image and $y_i$ is the label
Loss over the dataset is an average of loss over examples:
\[
L=\frac{1}{n_{train}}\sum_i L_i(f_{W,b}(x_i), y_i)
\]
Convert Scores into Probabilities by Softmax
Want to interpret raw classifier scores as probabilities
- Use the shorthand for the score vector: $s=f_{W,b}(x_i)$
- Turn $s$ into the predicted probability that a data belongs to class $k$ by the softmax function: \[ P(Y=k|X=x_i)=\frac{e^{s_k}}{\sum_j e^{s_j}} \]
cat
car
frog
car
frog
3.2
5.1
-1.7
5.1
-1.7
$\xrightarrow{\text{exp}}$
Probabilities must be >= 0
24.5164.0
0.18
$\xrightarrow{\text{normalize}}$
Probabilities must sum up to 1
0.130.87
0.00
Negative Log-Likelihood Loss
- We would like the probability of the groundtruth class to be maximized.
- Negative Log-Likelihood loss: Minimize $-\log P(Y=y_{groundtruth}|X=x_i)$ is equivalent to maximizing the predicted probability of the groundtruth class: \[ L_i=-\log\left(\frac{e^{s_{y_{groundtruth}}}}{\sum_j e^{s_j}}\right) \]
cat
car
frog
car
frog
3.2
5.1
-1.7
5.1
-1.7
$\xrightarrow{\text{exp}}$
Probabilities must be >= 0
24.5164.0
0.18
$\xrightarrow{\text{normalize}}$
Probabilities must sum up to 1
0.130.87
0.00
$\xrightarrow{-\log}$
Loss: $-\log P(Y=y_{groundtruth}|X=x_i)$
$L_i=-\log(0.13)=2.04$
Summary of Building the Log-Likelihood Loss
Given a training dataset $\{(x_i,y_i)\}_{i=1}^n$.
- $f(x;\theta)$ to denote the classifier (e.g., linear classifier) parameterized by $\theta$.
- $f_i(x;\theta)$ to denote the score for the $i$-th class
- Then the loss function is \[ L(\theta)=-\frac{1}{n}\sum_{i=1}^n \log \left(\frac{e^{f_{y_i}(x_i;\theta)}}{\sum_j e^{f_j(x_i;\theta)}}\right) \]
Numerical Trick for Computing Log-Likelihood
\[
L(\theta)=-\frac{1}{n}\sum_{i=1}^n \log \left(\frac{e^{f_{y_i}(x_i;\theta)}}{\sum_j e^{f_j(x_i;\theta)}}\right)
\]
- One issue is that we need to compute the exponential of $f_j(x;\theta)$, which may cause numerical issues (overflow) if some $f_j(x;\theta)$ is big.
- Trick:
- Let $t=\max_j f_j(x;\theta)$, then \[ L(\theta)=-\frac{1}{n}\sum_{i=1}^n \log \left(\frac{e^{f_{y_i}(x_i;\theta)-t}}{\sum_j e^{f_j(x_i;\theta)-t}}\right) \]
- Note that $f_j(x_i;\theta)-t\le 0\ \forall j$, so $e^{f_j(x_i;\theta)-t}$ will not overflow
Optimization
Gradient Descent for Numerical Optimization
Consider the general optimization problem:
\[
\begin{aligned}
&\underset{x}{\text{minimize}}&& f(x)
\end{aligned}
\]
Gradient Descent for Our Loss Minimization
Recall that our classifier training should minimize the following loss function:
\[
L(\theta)=-\frac{1}{n}\sum_{i=1}^n \log \left(\frac{e^{f_{y_i}(x_i;\theta)}}{\sum_j e^{f_j(x_i;\theta)}}\right)
\]
# Vanilla Gradient Descent
weights = random_init() # e.g., sample a vector from Gaussian distribution
while True:
weights_grad = evaluate_gradient(loss_fun, data, weights)
weights += -step_size * weights_grad # perform parameter update
Stochastic Gradient Descent
\[
L(\theta)=-\frac{1}{n}\sum_{i=1}^n \log \left(\frac{e^{f_{y_i}(x_i;\theta)}}{\sum_j e^{f_j(x_i;\theta)}}\right)
\]
Limitation of Gradient Descent (GD)
- In GD, gradient computation needs to average the gradient of every data sample.
- If the dataset is large, gradient computation will be very slow!
- A very simple modification to GD
- At every step, randomly sample a minibatch of data points (e.g., 256 data points)
- Compute the average gradient on the minibatch to update $\theta$
Stochastic Gradient Descent
# Vanilla Stochastic Gradient Descent
weights = random_init() # e.g., sample a vector from Gaussian distribution
while True:
data_batch = sample_training_data(data, 256) # sample 256 examples
weights_grad = evaluate_gradient(loss_fun, data_batch, weights)
weights += -step_size * weights_grad # perform parameter update
SGD with Momentum
Here’s a popular story about momentum [1, 2, 3]: gradient descent is a man walking down a hill. He follows the steepest path downwards; his progress is slow, but steady. Momentum is a heavy ball rolling down the same hill. The added inertia acts both as a smoother and an accelerator, dampening oscillations and causing us to barrel through narrow valleys, small humps and local minima.
SGD with Momentum
SGD with Momentum
\[
\theta^t = \beta \theta^{t-1} - (1-\beta) \alpha g
\]
$\alpha$: learning rate (e.g., $\alpha = 1e-4$)$\beta$: momentum (e.g., $\beta=0.9$)
$g$: gradient

Left — SGD without momentum, right— SGD with momentum.
Example
Consider a 3-category classification problem (colored dots as training data).


Intepretation
- Recall $f_{W,b}(x)=Wx+b$, where $W=\begin{bmatrix}w_1^T\\w_2^T\\w_3^T\end{bmatrix}$.
- Therefore, the score for each category are \( \begin{cases} f_1=w_1^Tx+b_1\\ f_2=w_2^Tx+b_2\\ f_3=w_3^Tx+b_3\\ \end{cases} \)
- After learning, we obtain the $w_i$'s to minimize the negative log-likelihood loss
Intepretation
- Colored lines: line equations of \[ \begin{align} 0&=w_1^Tx+b_1\\ 0&=w_2^Tx+b_2\\ 0&=w_3^Tx+b_3\\ \end{align} \]
- Vectors (normals of lines): $w_1$, $w_2$, and $w_3$
- $w_i$'s point to the direction that $f_i$'s give higher scores

Intepretation
- Colored regions: Where $f_i$ is higher than the scores of other categories
- Note that, the decision boundary between two categories are straight lines

Decision Boundary for Binary Classification
- Binary classification: When there are only two categories
- Decision boundary: A simple straight line
Hard Cases for a Linear Classifier

End
