Introduction to Computer Vision

Hao Su

Fall, 2021

Agenda

click to jump to the section.

Applications of Computer Vision

Have you ever used computer vision?
How? Where?

Optical Character Recognition (OCR)

Technology to convert scanned docs to text

https://lens.google/

Face Detection

Almost all digital cameras detect faces

Login Without a Password (Face ID)

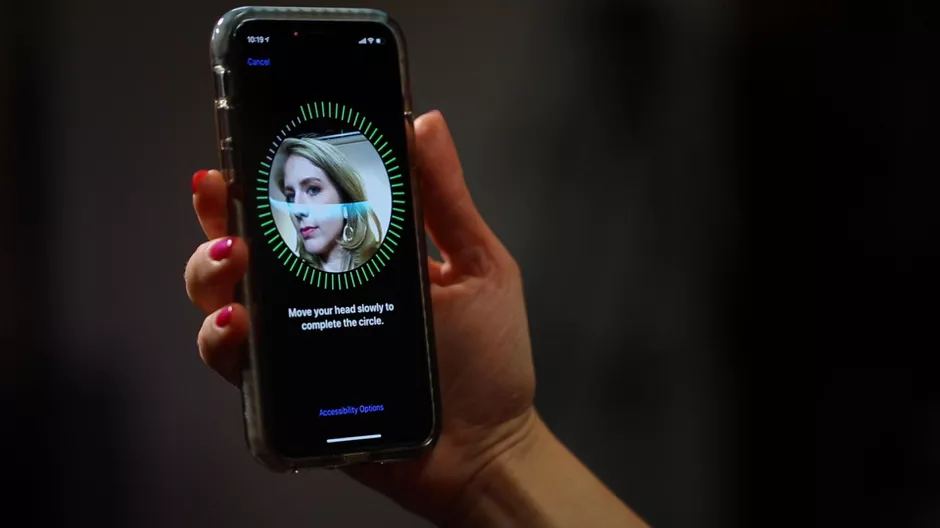
Face Spoofing Detection

3D from Images

Building Rome in a Day: Agarwal et al. 2009

Special Effects: Movie-making

Sports

https://ca.victorsport.com/index.html

Medical Imaging

Autonomous Driving

https://www.ptolemus.com/topics/autonomous-vehicles/

Autonomous Driving

3D LIDAR Sensor

Industrial Robots

Vision in Space

Augmented Reality and Virtual Reality

Jitendra Malik, UC Berkeley
Three R's of Computer Vision

[Further progress in] the classic problems of computational vision:

reconstruction
recognition
(re)organization

[requires us to study the interaction among these processes].

Teaching Plan

Ridiculously Brief History of Computer Vision

1966: Minsky assigns computer vision as an undergrad summer project
1960's: interpretation of synthetic worlds
1970's: some progress on interpreting selected images
1980's: ANNs come and go; shift toward geometry and increased mathematical rigor
1990's: face recognition; statistical analysis in vogue
2000's: broader recognition; large annotated datasets available; video processing starts
2010's: Deep learning with ConvNets
2031: My very own robot?

Computer Vision and Nearby Fields

Derogatory summary of computer vision:
Machine learning applied to visual data.

Goal

Focus on the classics of computer vision. Will briefly cover deep learning for vision in the last few weeks
Basic paradigm of lectures:
- Convert a vision problem to a set of mathematical equations
- Write a program to solve the equations

Syllabus

Topics to cover:

Geometric Transformations
Camera Model
Multi-View Reconstruction
Video Tracking
Image Recognition

Basic Mathematical Tools

Matrix and Vector
Least Square Problem
Taylor's Expansion
Gradient of Multi-variable Functions

We will use these mathematical tools on and on.

Basic Programming Tools

Python
Matplotlib Library: Read images and draw figures
Numpy Library: Linear algebra
PyTorch Library: Deep learning

Related Courses in CSE

CSE152A Fall (Hao Su): Introductory level, linear equation systems centric
CSE152B Spring (Manmohan Chandraker): Advanced, deep-learning centric
CSE252A Fall (Ben Ochoa): Similar to CSE152A but with greater technical depth and breadth
CSE252B Winter (Ben Ochoa): 3D Reconstruction by Classical Methods
CSE252C Spring (Manmohan Chandraker): Research oriented
CSE291 Winter (Hao Su): 3D understanding by deep learning
CSE291 Spring (Hao Su): Robotics by deep learning

Exams and Assignments

Exams (20%)

A final project (by composing and tuning solutions from assignments)
No in-class exams

Homework (80%)

Programming and Q&A based problems
9 assignments (released weekly) without late days
You can drop 1 assignment without penalty
Expected time to solve all problems in each homework: $\sim 5$ hours
Each homework solicits your feedback on teaching (1 free credit)

Some extra credits

Collaboration Policy

You can work individually or form study groups of two members
For study groups,
- each individual must create and submit your own solution of all problems
- please clearly indicate the name of your collaborator and the problems you have discussed

Reference Book

https://szeliski.org/Book/

Test of Background

Gradescope

We will use Gradescope to provide feedback to your answers (for this homework, also for future assignments).
Invitation code: 6PWK23
Please submit your solution as a PDF file (either scanned from a paper or exported from a document editor).
Feel free to discuss with anyone if you do not know how to solve them, but you must write every line of your submission by yourself.
2 extra credits as long as you put (partial) answers to all problems (even with incorrect answers) and no plagiarism is identified.
Due: Sep 26 2021 11:59 PM

Background

Linear algebra
Calculus
Probability
Python

For each question

Write down the answer
Self-assess your confidence: Scale of 1 (lowest) to 3 (highest)

Linear Algebra

Q1: Consider the matrix $ A= \begin{bmatrix} x & x^2\\y & y^2 \end{bmatrix} $

What is the rank $A$ when $x=1$ and $y=2$?
What is the rank $A$ when $x=0$ and $y=1$?
What is the null space of $A$ when $x=2$ and $y=2$?

Linear Algebra

Q2: Consider the matrix $ A= \begin{bmatrix} 1 & 0 \\ 2 & 4 \end{bmatrix} $

What is the transpose of $A$?
Define eigenvalues and eigenvectors of a matrix.
What are the eigenvalues of $A$?
What are the eigenvalues of $A^2$? Are they the same as the eigenvalues of $A$? Why?

Linear Algebra

Q3: Suppose that $ y=x^T \begin{bmatrix} 1 & 2 \\ 2 & 1 \end{bmatrix}x $, where $x\in\R{2}$.

Expand the expression as the polynomial of $x_1$ and $x_2$.

Linear Algebra

Q4: Suppose that $y=3x_1^2+5x_1x_2+4x_2^2$.

Rewrite the expression as $y=x^T A x$ where $A\in\R{2\times 2}$ and $A=A^T$.

Linear Algebra

Q5:
(a) Given two vectors, $a=[1, 2, 3]$ and $b=[-1, 0, 1]$

What is the dot product $a\cdot b$?

(b) If $R$ is a $3\times 3$ rotation matrix, what is $R^TR$?

Calculus

Q6:

What is the derivative of $f(x)=x^2$?
What is the partial derivative of $f(x,y)=x^2y$ with respect to $y$?
What is the gradient of $f(x,y)=x^2y$?
State the chain rule of differentiation

Calculus

Q7: What is the Hessian matrix of $f(x,y)=x^2y$?

Calculus

Q8:

What is the Taylor's expansion of $f(x)=e^{3x+1}$ (up to the second order, i.e., $f(x)\approx ax^2+bx+c$)?
What is the Taylor's expansion of $f(x_1,x_2)=e^{3x_1+x_2}$ in matrix form (up to the second order, i.e., $f(x)\approx x^T A x + Bx + C$)?

Python

Q9:

Have you used Python in the past?
Briefly describe a program or project you wrote in Python.
Write a snippet: Use a loop to print numbers from 1 to 10.
Have you used Numpy in the past?

Feeling of Background Test

Q10:

What is the total time you use to finish the background test?
How difficult are the problems?
- A: Very easy, a piece of cake
- B: Modest, but I can deal with them with a bit of efforts
- C: Hard, not as expected
When (year and quarter) and which courses (course number) did you take to cover materials we tested?
Do your previous courses cover all the tested materials? If not, which problem is not covered?

Your Expectation

Q11: What is your expectation of this course?

A: Rigorous (and difficult) course. I would read significant extra materials to become an expert and find jobs in computer vision or related fields.
B: Modest course. Cover basic concepts and algorithms. I can spend time to learn about the details of how computer vision works, but I prefer to read as few external materials as possible before working on homeworks.
C: Elementary course: Cover ideas and intuitions. I just want to call existing libraries to do projects. I am not interested in how the algorithms behind the functions are invented and implemented.

End